Post Your Answer
Post Your Answer
Post Your Answer
Ans 1: (Master Answer)
Class : Class 1
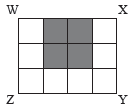
(A): Shaded area = Area of 4 small squares = 144 sq. m
Area of 1 small square = 144 ÷ 4 = 36 sq. m
Side of small square = 6m
WZ = XY = 3 x 6 = 18m
WX = ZY = 4 x 6 = 24m
Perimeter of rectangle = 2 x (18 + 24)
= 84 m
Ans 3:
Class : Class 8
Shaded area = Area of 4 small squares = 144m2Area of 1 small square = 144 ÷ 4 = 36m2Side of small square = = 6mWZ = XY = 3 x 6 = 18mWX = ZY = 4 x 6 = 24mPerimeter of rectangle = 2 x (18 24)= 84cm
Post Your Answer
Post Your Answer
Post Your Answer
Ans 1:
Class : Class 9
It is 74 itself. Think of it like this: You have Rs. 9.7 with you and you want to buy as many chocolates as possible. In such a case, you can buy only 4 chocolates, as you are short of Rs. 0.3. Dividing 9.7 by 2 gives 4.85 that can be approximated to 5, which is wrong as 5 chocolates require Rs. 10 (you need Rs. 0.3 more). So, you can use the amount less than or equal to what you have with you.