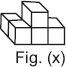
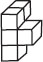
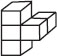
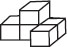
Post Your Answer
Ans 4:
Class : Class 9
all b,c,d are correct according to the the question which states "select the the INCORRECT option"
Ans 12:
Class : Class 6
CC means 200,X means 10 and VII means 7(5 1 1)............ So, the number that was to match was 207 but here it is 217,there shouldn't have been X because X made it 17 instead of 207,so the answer is C
Ans 14:
Class : Class 5
I think that the mistake is in the question he was going to ask the correct match and by mistake he has written "choose the INCORRECT ONES.
Ans 18:
Class : Class 8
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
Ans 19:
Class : Class 6
The answer is c because they are asking us to find the wrong numeral and 207 is CCVII whereas in the question it is CCXVII
Ans 23:
Ans 24:
Post Your Answer
Post Your Answer
Post Your Answer
Post Your Answer
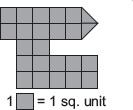
How many right angles are formed when hour hand of a clock moves from
(A) 2 to 8 (B) 6 to 9
| (A) | (B) | |
| A | 1 | 1 |
| B | 1 | 2 |
| C | 2 | 2 |
| D | 2 | 1 |
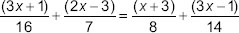
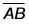 = 6cm,
= 6cm,  = 4cm, and diagonal
= 4cm, and diagonal 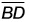
 ABCD is the required parallelogram.
ABCD is the required parallelogram.