Post Your Answer
Post Your Answer
Post Your Answer
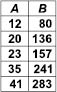
Ans 7:
Post Your Answer
Post Your Answer
Ans 6:
Class : Class 9
Correct answer is 8:45 am
Ajay arrived at 8:30 am and that time is 15min earlier than usual so usual time is 8:30+15 min is equal to 8:45