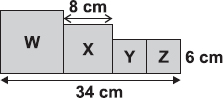
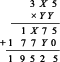Ans 4:
Post Your Answer
Post Your Answer
Post Your Answer
Ans 1: (Master Answer)
Class : Class 1
Volume of 1 cube will be 2x2x2=8 units
Volume of 12 such cubes is 12x8= 96 units.
The correct answer is D.
Post Your Answer
Post Your Answer
Ans 5:
Class : Class 2
so so so so so so wrong. They wont even let us put this as an error, when we put this as an error, it will say 'Please enter valid error' when it is a valid error. So bad SOF.
Ans 6:
Class : Class 5
Whole question is wrong. The solution is also wrong. The 'squares' in the question and the solution has to be changed to 'triangles. The only thing which was right is the diagram in the solution.
Ans 8:
Class : Class 7
yes,b is the right answer. we should just turn the diamond little bit. it will become square. and the other 5 squares.
Ans 15:
Class : Class 4
It should be 6 as the first one is the outer square(biggest one) and there are 4 small squares inside it, which makes 5 squares. There is also one square inside the figure which is tilted. It looks like a rhombus but isn't a rhombus because a rhombus doesn't have 4 angles measuring 90 degrees.
Ans 16:
Class : Class 6
The correct answer is C because one is the outer square, then there are 4 squares inside it and one square is tilted so that will also count.
Ans 17:
Class : Class 8
B as the rhombus if turned slightly diagonally will form a square and 5 squares are already there
Post Your Answer
Post Your Answer
Ans 5:
Class : Class 8
i attempted this question and it was showing green also CHEATER PETER STRAWBERRY EATER (SOF's new name) [short form- CPSE]