Post Your Answer
Ans 1: (Master Answer)
Class : Class 1
(D)
Number of oranges Sanjeev bought = 2160
Number of rotten oranges = 46
Number of remaining oranges = 2160 – 46 = 2114
Oranges in each box = 2114 ÷ 7 = 302
Post Your Answer
Post Your Answer
Ans 7:
Class : Class 6
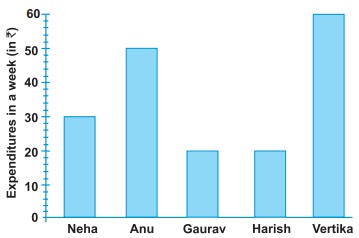
Actually you all got b because you only counted Anu's savings and not Gaurav's saving. I mean that Gaurav already has R12, so if anu gives him 12 more rupees then both of them have equal. Is a bit tricky but not complicated.
Post Your Answer
Post Your Answer
Post Your Answer
Post Your Answer
Ans 1:
Class : Class 2
Number of cups 4 bottles can fill = 4 x 3 = 12Number of kettles 12 cups i.e. 4 bottles can fill = 12 ÷ 4 = 3CloseNumber of cups 4 bottles can fill = 4 x 3 = 12Number of kettles 12 cups i.e. 4 bottles can fill = 12 ÷ 4 = 3Close
Ans 2: (Master Answer)
Class : Class 1
(C)
Number of cups 4 bottles can fill = 4 x 3 = 12
Number of kettles 12 cups i.e. 4 bottles can fill = 12 ÷ 4 = 3

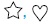 and
and 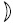 respectively.
respectively.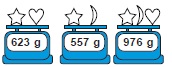
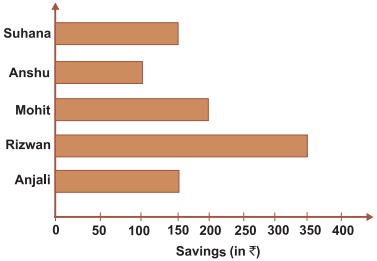




 .
.