Post Your Answer
Post Your Answer
Ans 1:
Class : Class 10
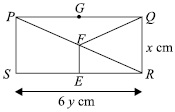
THERE ARE 4 LINES OF ROTATIONAL SYMMETRY.BUT THERE IT IS ASKED THAT WHAT IS THE VALUE OF 2*K.WE KNOW THAT 2*K IS TOTAL NUMBER OF ROTATIONAL SYMMETRY.SO:-
2*K=4
K=4/2
K=2
Post Your Answer
Post Your Answer
Post Your Answer
Post Your Answer
Ans 2: (Master Answer)
Class : Class 1
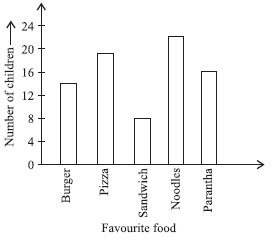
(A): Number of children who like pizza and parantha together = 19 + 16 = 35
Number of children who like burger and parantha = 14 + 16 = 30
Hence, 35 - 30 = 5 more children like pizza and parantha together than of burger and parantha together.