Subject :IMO Class : Class 7
The length of a rectangular plot is twice its width. If the length of its diagonal is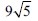 
metres, the perimeter of the rectangle is
A27 m
B54 m
C81 m
D80 m
Ans 1:
Class : Class 9
give explanation please.
Ans 2:
Class : Class 6
Ans 3:
Class : Class 7
it is very simple and can be solved with Pythagoras.Length=2y Breadth=yroot of [(2y)square ysquare]=9 x root of 5root of [4ysquare ysquare]=9 x root of 5root of 5ysquare=9 x root of 5 = y x root of 5thus y = 9 and 2y = 18p=54
Ans 4:
Class : Class 7
please provide explanation soon
Ans 5:
Class : Class 7
Sorry diagonal of a rectangle is l^2 b^2
Ans 6:
Class : Class 9
explaination of answer not provide....how to check the solution??
Ans 7:
Class : Class 8
pl give solution, very confusing question
Ans 8:
Class : Class 7
w=xl=2xd=9root52(l b)=?2(x 2x)=?using pythogras theorem,xsquare 4 x square=(9root5)squared5xsquare=405x square=81x=9hence substitute values with x,perimeter=54
Ans 9:
Class : Class 9
This can be solved like this: take length as 2x and breadth as x. Applying the pythagoras theorem, (x)^2 (2x)^2 = (9 * root 5)^2. Equal to x squared 4x squared = 9 squared * root 5 squared 5x squared = 81 * 5. 5 and 5 cancel on both sides. x squared = 81 x = 9 = breadth 2x = 18 = length perimeter = 2 (l b) 2 * 27 = 54
Ans 10:
Class : Class 7
First of all,diagonal of a rectanhle=square root of l^2 b^2,so 9Ãsquare root of 5 is square root of 81 Ã 5 that is 405 so here 2x is l and x is b.if i m taking l is 18 and b is 9 and squaring them we get 405 so perimeter of the rectangle is 2(18 9) that is 54.