Simplify :
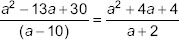
A a2 – 8a – 20 = 0
B a2 + 30a – 40 = 0
C a2 – 80a – 30 = 0
D a2 + 7a – 30 = 0
answer is a -10
Ans 1:
Class : Class 9
a2 - 13a + 30 = a2 + 4a + 4
a - 10 a + 2
=> (a2 - 13a + 30)(a + 2) = (a2 + 4a + 4)(a - 10)
=> a3 + 2a2 - 13a2 - 26a + 30a + 60 = a3 - 10a2 +4a2 + 4a - 40
=> - 11a2 + 4a + 60 = - 6a2+ 4a - 40
=> - 11a2 + 6a2 + 60 + 40 = 0
=> - 5a2 + 100 = 0
=> 5a2 = 100
=> a2 = 20
=> a = √20
Insert the value of'a'and you will get the answer.
Ans 2:
Class : Class 8
By factorization process, we get a-3 = a 2, which is in fact a linear equation without a solution. On the other hand, by solving through cross multiplication method (as shown in the solution of this question), we get a²-8a-20 = 0, or (a 2)(a-10) = 0. By solving the quadratic equation, we get a as (-2) or (10), which, upon substituting in the formula given in the question, doesn't satisfy the equation. This is because the equation in the above question isn't even actually correct, as (a-3) is not equal to (a 2), as that would lead to the statement: 5 = 0, which is obviously not true.
Ans 7:
Class : Class 9
This question is completely wrong as when we factorise (a^2-13a 30) and (a^2 4a 4), we get (a-3)(a-10) and (a 2)^2 respectively. After calculating more, we get a-3=a 2 which has no solution as -3â 2
Ans 8:
Class : Class 4
The question is wrong.If A is the answer, solving this quadratic eqn, we get a=10 or -2since the answer is a simplified form of the question, these values of a should also hold for question also. But if we put these vales in the question either LHS or RHS denominator will become 0 making it undefined.the actual procedure is to factorize.=> [(a-3)(a-10)]/(a-10)=[(a 2)(a 2)]/(a 2)=> a-3 = a 2=> -3 = 2 which is absurd. so the question is wrong.